Hi Sarah,
I have a question that's been bugging me for years. It's a two-fold question relating to the same scenario. Say I would like to accelerate to a specific speed while going up a hill with a moderately steep grade. I either continue in the higher gear I'm already in but that's not in the ideal powerband, and let the engine build speed slowly; or I drop into a lower gear that's in the right powerband range, get to my desired speed and hold the throttle at a constant RPM once I'm there. My first question is: which is better for fuel economy? My second question is: which is better for the longevity of the engine? I have my own theories on the matter, but I'd much prefer your expert opinion.
Cheers!
Sean
Great question Sean- I can use my mad Excel skills! If math and graphs weren't your thing in school, you can skip to the end for the answer without all the boring details. We really have to look at the components that contribute to fuel consumption in controlled environments to understand what their individual impact is.
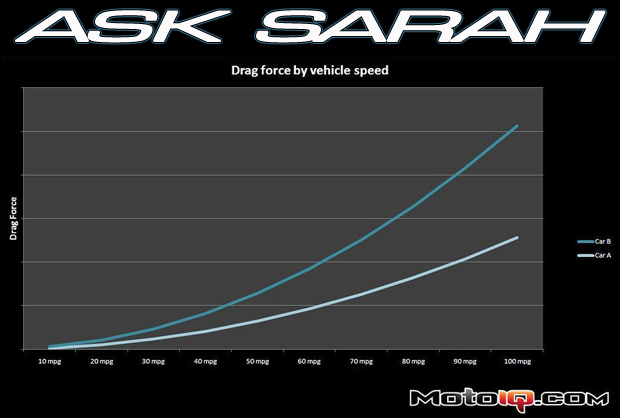
One factor affecting fuel economy is the force of drag- not the RuPaul kind! Air resistance can be calculated by 1/2 of the car's coefficient of drag (Cd) x the surface area of the front of the car (A) x the density of air * (r) times the speed of the car (v) squared.
Air resistance = 0.5 (Cd x A)(r x v^2)
Holding the coefficient of drag and the surface area of the front of the car constant (assuming you're talking about driving the same car), drag force increases exponentially as vehicle speed increases. So if you accelerate more quickly to get up to that higher speed, you'll need more power and consume more fuel to overcome the greater drag force at that speed for the longer period of time, versus getting up to speed slowly. Simply put, lower speeds = lower fuel consumption. Chalk one point for accelerating to your speed more slowly.
 |
| This is a comparison of two vehicles- Car A has a 0.27 coefficient of drag and Car B has a 0.32 coefficient of drag. Both assume constants for other variables, such as 68 degrees ambient temperature, sea level, and 26ft squared front surface area. Notice how the drag force increases exponentially as speed increases and especially how much greater the force is for the car with the larger coefficient of drag. This variance between the two cars also increases with speed. |
Air density is one variable that is needed in order to calculate drag force. Air density is impacted by altitude, ambient temperature, and humidity. Air density increases with increased air pressures but air density decreases with higher temperatures, higher altitudes, and to a lesser extent, increased humidity. A lower air density reduces drag and aerodynamic lift but can lead to lower engine horsepower since it reduces the amount of oxygen available for combustion.
Air/Fuel ratio also plays into fuel consumption. For gasoline engines, the stoichiometric air/fuel ratio is 14.7:1. Stoichiometric refers to the ideal ratio of fuel and oxygen from the air that leads to complete combustion. This is also where a 3-way catalyst runs the most efficient at keeping emission output low. At light throttle cruising conditions, most engines are tuned close to a stoichiometric 14.7:1 air/fuel ratio. A leaner air/fuel ratio (ie. 16.5:1) will consume less fuel than a richer a/f (12.5:1); less parts fuel per unit of air.
You can calculate an assumption of fuel consumption (not including the impact from increased drag forces) at various speeds if you know mass air flow of the engine, an equation involving air density, engine displacement, rpm, and volumetric efficiency.
Fuel consumption (fuel mass) = Engine mass air flow / A/F ratio
We can use adequate assumptions for some of these variables in order to map fuel consumption for illustrative purposes. Without turning this answer into a book going through all the calculations and unit conversions, I'm leaving units out of this graph just to show the relationship. FYI, I used a naturally aspirated SR20DE engine since I've used these variables for similar calculations in the past so I have the data on hand.
 |
| This is a fuel consumption graph that shows fuel mass used between 20 and 80mph in 10 mph increments, in both 3rd and 4th gears for this example. You can see by this graph how using 3rd gear will consume more fuel than 4th gear. |
This graph shows how speed affects fuel consumption during closed loop operation when the ECU uses input from the oxygen sensor to maintain close to a 14.7:1 ratio for all conditions. However, there are open loop situations such as cold engine operation or heavy loads or wide open throttle where the engine ignores the O2 sensor inputs and adjusts the mixture to be leaner or richer than the ideal ratio. At wide open throttle for instance, the mixture runs closer to a richer 11.5-12.7:1 air/fuel ratio, which helps to keep the engine cool and less prone to detonation. Many factory turbocharged cars are programmed even richer at wide open throttle. Since the engine is usually tuned for a richer air/fuel mixture when accelerating or under heavier loads or at wide open throttle, that's another point for slower acceleration.